进行化工原理实验,首先遇到的是实验设备的使用问题,其次是测取数据的问题,第一个问题散见于各个实验中。下面介绍带有共性的问题,例如,应该测取哪些数据?如何读取和记录?记录的数据又如何整理、分析为实验结论等等。
一、实验中应测取哪些数据
1、凡是影响实验结果或者数据整理过程所必需的数据,都必须测取。它包括大气条件、设备有关尺寸、物料性质及操作数据等。
2、有些数据不必直接测取,可以从测取的某一数据导出或从手册中查到。例如测出水温后,可查出水的粘度和密度等数据。
二、读取和记录数据应注意的问题
1、事先必须拟好记录表格,表格应简明扼要而又符合实验内容的标题名称。
2、表格中应注明各项物理量的名称、符号及单位。化工数据中,有的数量很大或很小,如二氧化碳的亨利系数E,用科学记数法表示:20℃时,E=1.42×10-8[Pa]。当列表时,项目名称写为E×10-8,单位记作[Pa],而表中数字写为1.42,即E×10-8=1.42[Pa]。也可以如下法表示,项目名称为E,单位记作[×10-8Pa],表中数字仍为1.42。
3、实验时一定要等操作稳定后,才开始读数,条件改变后,要等操作再次稳定后再读数,不稳定情况下所读取的实验数据是不可靠的。
4、数据记录必须真实地反映仪表的精确度。一般要记录至仪表上最小分度以下一位数。例如温度计最小刻度为1℃,读出某一温度应为25.5℃,若温度恰好在25℃,也应写为25.0℃,有效数字为三位。
5、实验直接测量或计算的结果,该用几位数字表示,是件很重要的事。有人认为数值在小数点后面的位数越多越准确,其错误在于没有弄清小数点的位置与所用测量单位的大小有关,而与测量的准确性无关。例如长度记录为0.314m和314mm,其准确度完全相同。还有人认为,计算结果保留位数越多越准确,其错误在于不了解在一定仪表条件下,所测得数据只能具有一定的准确度,绝不应该过多地保留位数,以致使计算的准确度超过测量仪器的精度。例如传热实验中,蒸汽温度T=120.5℃,空气进、出口温度为24.4℃和79.7℃,则对数平均温度差△tm=64.6℃。若保留位数过多,写作△tm=64.55℃,则超出了温度计的测量精度,是不科学的。
三、实验数据的处理
记录下的原始数据通常要进行运算,或以列表法表示,或以图示法表示,或以经验公式表示。因此,取得实验数据后,还要正确地处理这些数据,才能获得应有的结果。
1、数据的运算
(1)在计算中应注意有效数字和单位换算。
(2)数据运算中应采用常数归纳法,即计算公式中的许多常数归纳为一个常数对待。例如管路计算中,由于流量改变而导致雷诺准数的改变,因为
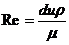 ,
, ,故
,故 。
。
计算时先求出B值,依次代入VS,即可求出相应的Re值。
2、数据处理
(1)列表法
利用列表法表达实验数据时,表头栏目应写明所测物理量名称、符号、单位,自变量选择时最好能使其数值依次等量递增。
(2)图示法
利用图示法表示实验数据有许多优点。首先它能清楚地显示所研究对象的变化规律与特点,如极大、极小、转折点、周期性等。其次可利用足够光滑的曲线,作图解微分和图解积分。第三可通过适当地坐标变换,求出经验方程式。图示法在化学工程实验数据整理中具有特殊重要的地位。下面将列专题介绍。
(3)经验公式法
实验数据用经验公式表达,使实验规律更加定量化。经验公式本身是客观规律的一种近似描述,是进一步探讨的线索和依据。
建立经验方程式的基本步骤如下:
①将实验测定的数据加以整理与校正。
②选出自变量和因变量,并绘出曲线。
③由曲线的形状,根据解析几何的知识,判断曲线的类型。
④确定公式的形式,并将曲线通过改变坐标方法,变换成直线关系。常见例子如表1所示。
⑤用图解法或解析法来决定经验公式中的常数。
表1 坐标变换示例表
方程式 |
变换 |
直线化后的方程 |
Y=axb Y=abx Y=aebx Y=ea+bx 

|
Y=lgy, X=lgx Y=lgy, X=x Y= lny, X=xY=lny, X=x 

|
Y=bx+lga Y=lgbx+lga Y=bx+lna Y=bx+a
Y=bx+a
Y=bx+a |
【示例1】在蒸汽—空气换热实验中,要将给热系数a与管内流速u的关系,整理成如下形式:
 即
即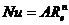
式中:a,管壁对空气的给热系数,W/(m2.K);
λ,空气的导热系数,W/(m.K);
d,管内径,m;
u,空气流速,m/s
ρ,空气密度,kg/m3;
μ,空气粘度,kg/(m.s);
Nu,努塞尔特准数;
Re,雷诺准数;
A、n,经验公式的系数。
数据记录如表2所示。
表2 传热数据记录表
序 号 |
流量示值 R,mm |
计前表压 P表,Pa |
热电偶示值,Et,mV |
蒸汽或壁 |
空气进口 |
空气出口 |
1 2 3 4 5 6 |
70.0 50.0 35.0 25.0 15.5 8.5 |
4080 3906 4599 5093 5960 6440 |
5.332 5.338 5.338 5.34 5.342 5.332 |
1.006 0.986 1.03 1.05 1.096 1.112 |
3.348 3.40 3.478 3.54 3.624 3.708 |
管径d=0.0178m,管长L=1.224m;流量系数C′=0.001233;室温t=13℃;大气压强Pa=101330Pa。
以第一组数计算举例。
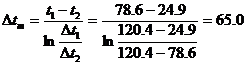
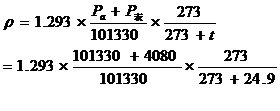
=1.233kg/m3

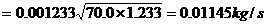
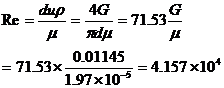
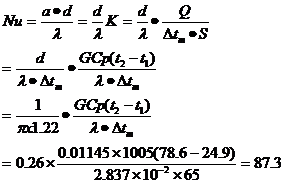
所有计算结果见表3。
表3 传热数据整理表
序
号 |
温度,℃ |
对数平 均温差 Δtm,℃ |
密度
ρ,kg/m3 |
质量 流量 G,kg/s |
雷诺数
Re |
努塞尔 特准数 Nu |
蒸汽,T |
进口,t1 |
出口,t2 |
1 2 3 4 5 6 |
120.4 120.5 120.5 120.5 120.5 120.5 |
24.9 24.4 25.4 26.6 27.4 26.2 |
78.6 79.7 81.4 82.7 84.6 86.4 |
65.0 64.6 63.0 61.9 60.1 58.6 |
1.233 1.234 1.237 1.240 1.246 1.250 |
0.01145 0.00969 0.00811 0.00687 0.00542 0.00402 |
41570 35160 29301 24801 19473 14443 |
87.3 76.3 66.2 57.7 47.4 36.8 |
用双对数坐标用图,如图1所示。
| |
|
| |
 |
由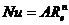
∴lgNu=nlgRe+lgA (1)
由图1得斜率
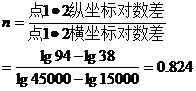
∴lgNu=0.824lgRe+lgA
将第一组数据代入上式,则
lgA=lg87.3-0.824×lg41570=-1.865
∴A1=0.0136

 分别将第二组至第六组数据代入,求得A2,A3,…,取平均值, A=0.0138
分别将第二组至第六组数据代入,求得A2,A3,…,取平均值, A=0.0138

 (2)
(2)
式(2)是用图解法得到的经验公式。此式亦可用最小二乘法计算。首先将方程(1)线性化处理:lnNu=nlnRe+lnA
令y=lgNu,x=lnRe,b=lnA
则y=nx+b
这就将指数关系转化为一元线性回归问题,根据一元线性回归原理:

式中:N,数据的组数,此题中N=6。
我们根据表3中的Re~Nu的6组数据,分别将Re与Nu取自然数,然后计算有关项目,并列在表4中。
表4 最小二乘法计算表
序号 |

|
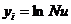
|
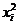
|
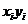
|
1 2 3 4 5 6 |
10.635 10.468 10.285 10.119 9.877 9.578 |
4.467 4.335 4.193 4.055 3.859 3.606 |
113.11 109.579 105.781 102.394 97.555 91.738 |
47.509 45.379 43.121 41.033 38.115 34.538 |
| |
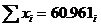
|
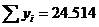
|
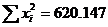
|

|

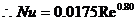 (3)
(3)
比较(2)和式(3),说明无论是图解法还是回归分析法,所得经验公式是一致的。
四、实验数据的图示法
常选横轴为自变量,纵轴为因变量。坐标分度的选择,要反映出实验数据的有效数字数位,并要求方便易读。分度坐标不一定从零开始,而应使图形占满坐标纸为宜。同一幅面上,可以有几种不同单位的纵轴的分度。不同纵轴的分度,应使曲线不至于交叉重叠。
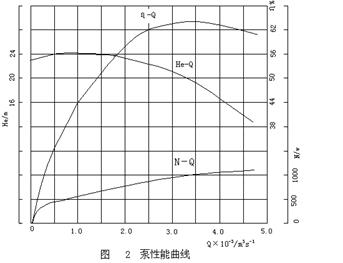
1、直角坐标图示法。化工原理实验中的干燥速率曲线、泵性能曲线和过滤曲线,均采用直角坐标图示法。本书以泵性能曲线的标绘为例,说明直角坐标图示法。
【示例2】泵性能实验测定的数据如表5所示。泵入口与出口管径为d=0.04m;真空计与压力表接口的垂直距离为h0=0.1m;水温t=20℃;查水的密度ρ=998kg/m3。
表5 泵性能实验数据表
序 号 |
流量 Q10-3m3/s |
真空度 mm |
压力 kg/cm2 |
实际功率 N,W |
扬程 He,m |
有效功率 Ne,W |
效率 η,% |
1 2 3 4 5 6 7 8 |
0 0.68 0.96 1.65 2.07 2.77 3.46 4.72 |
83 95 100 119 135 168 215 317 |
2.16 2.17 2.17 2.15 2.07 1.89 1.64 1.07 |
403 500 553 698 780 902 1007 1143 |
22.83 23.09 23.16 23.42 22.64 21.28 19.42 15.11 |
0 154 218 378 459 577 658 698 |
0 30.75 39.36 54.20 58.81 64.00 65.33 61.09 |
以第二组数据计算举例。由于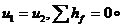
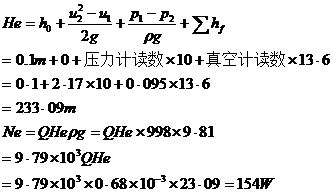
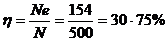
将表5中数据:He~Q,N~Q,η~Q分别标绘在图2中,得到泵性能曲线。
2、双对数坐标图示法。一般是横坐标与纵坐标均采用常用对数分度,在化学工程实验中应用十分广泛。例如,流体流动阻力实验中的λ~Re 曲线,吸收实验中△p~u曲线,传热实验中的Nu~Re曲线等等,均采用双对数坐标图示法。下面以流体流动阻力实验中λ~Re曲线的标绘为例,说明双对数图示法。
【示例3】流体阻力实验测定的数据,如表6所示。管内径d=0.04m;直管压点距离l=4m;水温t=20℃。
表6 阻力测定数据表
序 号 |
流量 Vs×10-3m3/s |
U管压差 R,mm |
雷诺数 Re |
直管压降 △p,Pa |
摩擦系数 λ |
1 2 3 4 5 6 7 8 |
3.5 2.5 2.0 1.75 1.5 1.25 1.0 0.75 |
81 42 27 21 16 12 8 5 |
110845 79062 63260 55224 47278 39332 31784 23838 |
10013.5 5192.2 3337.8 2596.1 1978.0 1483.5 989.0 618.1 |
0.0257 0.0262 0.0264 0.0269 0.0279 0.0303 0.0310 0.0343 |
以第三组数据计算举例。水温20℃时,查手册得:μ=1.005×10-3kg/(m·s);ρ=998.2kg/m3。
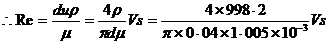
=3.163×107Vs=3.163×107×2×10-3=63260
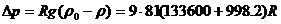
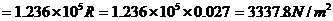


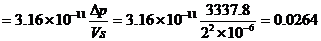
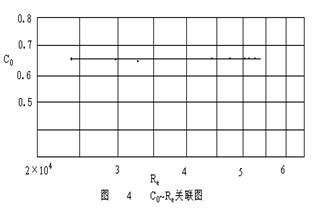
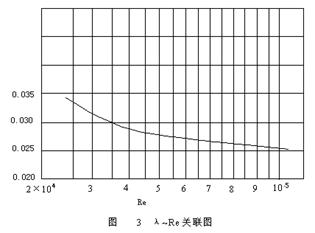
将计算结果也列在表6中,并将λ~Re关系,在双对数坐标纸上,标绘在图3中。
3、半对数坐标图示法。一般是横轴采用常用对数或自然对数分度,而纵坐标采用直角坐标分度。下面以孔板流量计的校正曲线为例,说明半对数坐标图示法。
【示例4】流量计校正实验测定的数据如表7所示。管径d=0.028m;孔板内径d0=0.028m;孔板内径d0=1.398×10-3m;水温t=19℃;查得水的密度ρ=998.2kg/m3;水的粘度μ=1.03×10-3kg/(m.s);计量槽底的面积0.5×0.3=0.15m2。
表7 流量计的测定数据表
序 号 |
流量 |
压差计 R,mm |
雷诺数 Re |
孔流系数 C0 |
计量槽水位高, m |
体积m3 |
时间s |
流量,Vs,m3/s |
1 2 3 4 5 6 7 8 |
0.20 0.20 0.33 0.30 0.20 0.20 0.20 0.20 |
0.03 0.03 0.0495 0.045 0.03 0.03 0.03 0.03 |
25 25.5 43 41.5 30 40 45 56.5 |
0.0012 0.00117 0.00115 0.00108 0.0010 0.00075 0.00067 0.00053 |
5799 543 525 458 381 229 172 110 |
51600 512000 51000 47500 44000 33000 29500 23500 |
0.653
0.657 0.661 0.671 0.649 0.669 0.661 |
以第二组数据计算举例。


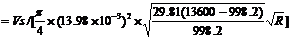
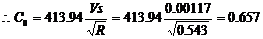

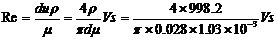


将计算结果也列在表7中,并将C0~Re关系,在半对当选坐标纸中,标绘在图4中。